一個最常見的 hyphothesis set 就是 perceptron, perception 就是把資料 進行線性組合,接著判斷是否大於某值決定結果, 例如:
每個 會對應到一個 ,我們要做的就是從所有 (也就是我們的 hypothesis set) 中找到最接近未知的 的那個,把這個東西視覺化大約是這樣:
為了表示方便我們把的 假裝後面偷藏一個 , 並且把 塞到 的後面。
這種把資料分成「是」或「不是」是 machine learning 重要的課題。
之後的表示中不寫波浪線了,另外,我們假裝不會發生剛好為零的資料。
舉一個實際 perceptron 例子,例如銀行有客戶的兩個資料「欠款數」跟「年收入」, 那麼可能來決定要不要借錢的的計算公式是:
- 「年收入」乘以三,減掉「欠款數」是否大於一百萬
- 若超過則借錢
- 反之不借
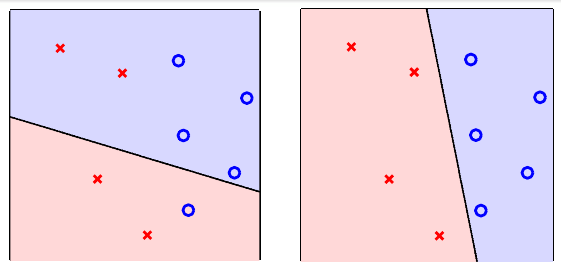
下面我們考慮一個最簡單的情形,假設有一筆資料是線性可分, 「線性可分的資料」的定義就是存在一個分割,兩邊的資料都正確歸類。 比較數學的說法就是 。 例如上面的資料就是線性可分,因為右圖的線把資料正確切兩半了。
對於這種資料,下面描述的演算法 perceptron learning algorithm (PLA) 可以找到這樣的線。
- 從任意的 開始:
- 找一個錯誤的資料
- 更新 ,
就這樣,為了計算量這裡對「找錯誤的資料」作更詳細的說明。
- 從任意的 開始:
- 從某個位置依序找一個錯誤的資料
- 已經繞一圈了都沒找到,那就是沒有錯誤了,可以結束。
- 找到了,下一次從這裡開始找。
- 更新 ,
這種循環檢查的方式讓 PLA 這個演算法的運算量很低。下面證明這個很簡單演算法一定會停止 (假設 是正確的分割):
首先因為 是正確的分割,,令 。
第一步我們觀察 跟 的內積關係:
速度大於線性漸增。
接著觀察 的長度
速度小於線性漸增,注意到會有這個現象是因為演算法總是選擇 的,也就是目前錯誤的點。
兩個合併起來就變成: 跟 的夾角